The unexpected maths problem at work during the Women's World Cup
 Getty Images
Getty ImagesIf you are in a room with 22 other people, it’s more likely than not that two of them share a birthday.
There was something strange about the recent Women's World Cup in Australia. If you were paying close attention, you might have spotted it. Many of the international teams had players who were born on the same day of the year – they shared birthdays.
What was going on?
There is a counterintuitive phenomenon known as "the birthday problem" or "the birthday paradox", which mathematicians like to use to confound our expectations. The problem is usually phrased along these lines: "How many people do you need to have at a gathering before the probability of at least two people sharing a birthday rises above 50%?"
Typically, when people are first posed this problem, they plump for a number like 180, which is roughly half the number of days in the year. This is because we tend to put ourselves in the room and think about the probability of someone else matching our own birthday. 180 is, in fact, way, way too many.
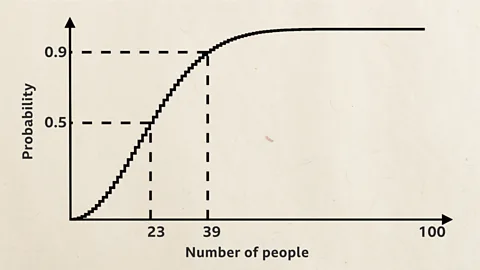
Making the reasonable assumption that birthdays are roughly evenly distributed throughout the year, the answer is just 23 people. This is because we are not concerned about the particular day on which the birthday falls, just that there is a match. By the time we have 39 people assembled the probability rises to nearly 90% (as you can see the graph below).
 Kit Yates/BBC
Kit Yates/BBCTo gain an insight into why the number required is so low, we can start by considering the number of pairs of people in the room – pairs of birthdays falling on the same day, after all, being what the question is about. With 23 people in the room it turns out there are 253 possible ways of combining them into pairs (see the diagram below). The exact calculation of the probability of a match is a little complicated, but perhaps – once we find out that 23 individuals gives rise to 253 pairs – it becomes less surprising that the probability of at least one pair with the same birthday rises above 50%. If there are more than 50 people, the probability of two sharing a birthday rises above 97%.
 Kit Yates/BBC
Kit Yates/BBCSo much for the theory, but does it work in practice? At the 2023 women’s world cup there were 32 squads taking part, each with exactly 23 players. It is the perfect test bed for the theory.
By crunching the data I was able to find that 17 (so just over half) of the 32 teams had at least two players who shared a birthday. Not perfect, but pretty close to the roughly 16 we would expect on average if we were to repeat the experiment multiple times.
Interestingly, only the Panamanian pair of Carmen Montenegro and Lineth Cedeño were born on exactly the same day of the same year (5 December 2000). Three squads (Brazil, Colombia and Denmark) had two pairs of shared birthdays and two squads (Morocco and Nigeria) even had three pairs. With their birthdays falling on Christmas Day, the aptly named Nigerian pair, Glory Ogbonna and Christy Ucheibe, have the second most common birthday across all the squads, with a total of seven people sharing the date.
You might also like:
In the second semi-final another birthday pairing lined up against each other. Late substitutes Alex Chidiac (for Australia) and Chloe Kelly (for England) share a birthday on 15 January, with Kelly exactly a year older than her counterpart. England midfielder Jordan Nobbs and her opponent Spanish forward Esther Gonzalez were born on exactly the same day (8 December 1992). Despite being in the squad, neither of them made it onto the pitch when England faced Spain in the World Cup final.
In total I identified 24 pairs of birthdays within the teams (coincidentally just over the magic number - 23), so the same "birthday reasoning" suggests that there is – more likely than not – a pair of pairs among these dates too. And indeed, the 3 March is the birthday of both a Danish pair (Simone Boye Sørensen and Luna Gevitz) and a Colombian pair (Sandra Sepúlveda and Diana Ospina Garcia). It turns out that 3 March is the most popular birthday across all squads, with a total of nine players sharing that anniversary.
Away from football, the same "birthday problem" reasoning can help us to explain seeming paradoxes in other fields. In 2001, while searching through Arizona’s state DNA database of 65,493 samples, scientists discovered a partial match between two unrelated DNA profiles. For two given unrelated individuals we would only expect a match of this calibre roughly once in every 31 million pairs of profiles sampled. This shock finding, which the researchers presented at a scientific conference, prompted a search for more possible matches. Upon comparing all the database’s profiles, 122 pairs of individuals with a similar or even greater degree of resemblance were identified.
 Getty Images
Getty ImagesBased on this study and now doubting the uniqueness of DNA identifiers, lawyers across the US argued for similar comparisons to be made in other DNA databases, including the national DNA database containing 11 million samples. If 122 matches had turned up in a database as small as 65,000 people, could DNA really be relied upon to uniquely identify suspects in a country with a population of 300 million? Were the probabilities associated with DNA profiles incorrect and therefore risking the safety of DNA-based convictions across the nation? Some lawyers believed so and even submitted the Arizona findings as evidence in order to cast doubt on the reliability of the DNA evidence in their defendants’ trials.
In fact, we can work out that comparing each of the 65,493 samples in the Arizona database with every other gives a total of over two billion unique pairs of samples. With a probability of one match per 31 million pairs of unrelated profiles we should expect 68 partial matches. The difference between the expected 68 matches and the 122 that were found might easily be explained by the profiles of close relatives in the database. Relatives' profiles are significantly more likely to throw up a partial match than those of unrelated individuals. Rather than shaking our confidence in DNA evidence, the database findings agree quite nicely with "birthday" mathematics.
The unexpectedly large numbers of pairwise combinations thrown up by birthday-type problems are frequently the driving force behind the huge numbers of possibilities which allow seemingly unlikely events to occur purely by chance. It’s worth remembering in situations like these, that when there are enough possibilities for an event to occur, even if the chance of any one of them occurring seems low, together they can make even seemingly improbable events become overwhelmingly likely.
--
